Dijkstra algoritm (다익스트라 알고리즘)

개요

음의 가중치가 없는 그래프에서 한 노드에서 다른 모든 노드까지의 최단거리를 구하는 알고리즘이며, 방향그래프, 무방향 그래프 모두 상관 없으나, 가중치가 음수인 edge가 단 하나라도 존재하면 이 알고리즘은 사용할 수 없다.

  • 우선순위 큐를 사용 하지 않는 최초 모델의 경우 O(N 제곱)이다.

  • 우선순위 큐(힙)을 사용 하는 경우 O(ElogN)이다.

  • 최단경로를 구하는 다른 알고리즘은 플로이드-워셀 알고리즘은 가능한 모든 쌍에 대한 최단 거리를 구하는 알고리즘인 반면, 다익스트라 알고리즘은 시작노드로 부터의 최단 경로를 구한다. (대신 수행 속도가 더 빠르다)

  • 다익스트라 알고리즘을 확장시킨 알고리즘이 A 알고리즘이다.

  • 가능한 적은 비용으로 가장 빠르게 도달하는 경로를 찾아내는 대부분의 문제에 응용된다.

알고리즘

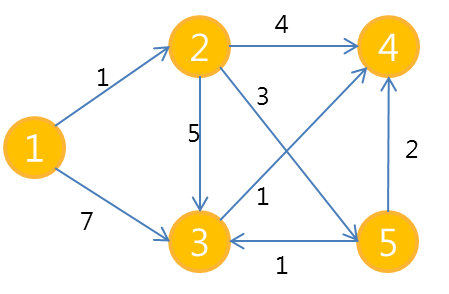
graph.png

  1. 출발점으로 부터의 최단거리를 저장할 배열 DIST를 만들고 모든 노드를 미방문(큰 값: Ingeter.MAX_VALUE)) 상태로 표시한다.

    NODE 1 2 3 4 5
    DIST 0 MAX MAX MAX MAX
    Check true false false false false

  2. 시작노드를 최초 방문노드로 설정한다(t = 0)

  3. 방문노드(t)에서 미방문 인접 꼭짓점을 찾아 DIST 배열을 업데이트 하고, 미방문 노드중 거리가 가장 짧은 노드(DIST[1])를 다음 방문노드로 결정(t = 1)한다.

    NODE 1 2 3 4 5
    DIST 0 1 7 MAX MAX
    Check true true false false false

  4. 모든 노드를 방문할 때까지 3의 과정을 반복 수행한다.

    NODE 1 2 3 4 5
    1 0 MAX MAX MAX MAX
    1->2 0 1 7 MAX MAX
    1->2->5 0 1 6 5 4
    1->2->5->4 0 1 5 5 4
    1->2->5->4->3 0 1 5 5 4
    DIST 0 1 5 5 4
    Check true true true true true

  5. DIST에 시작노드로 부터의 각 노드의 최단거리가 저장된다.

우선순위 큐 사용

우선순위 큐를 사용하여 다음 방문노드를 결정하면 O(ElogN)으로 시간복잡도가 줄어든다.

깃헙에서 소스 보기